AI Research
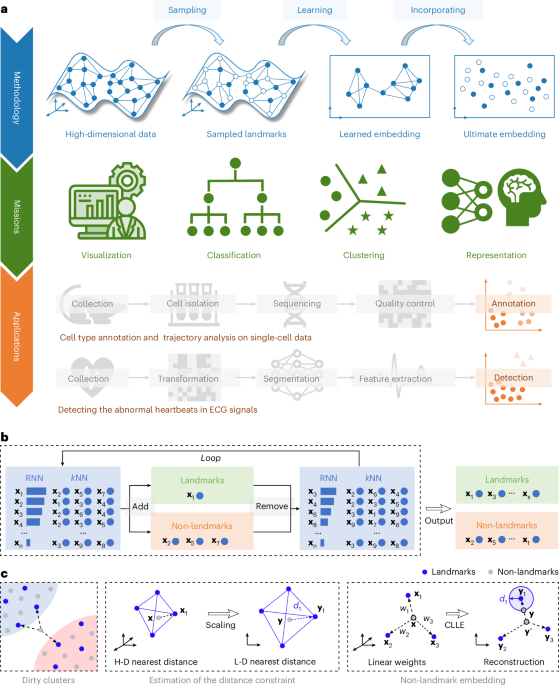
Sampling-enabled scalable manifold learning unveils the discriminative cluster structure of high-dimensional data
Busch, E. L. et al. Multi-view manifold learning of human brain-state trajectories. Nat. Comput. Sci. 3, 240–253 (2023).
Floryan, D. & Graham, M. D. Data-driven discovery of intrinsic dynamics. Nat. Mach. Intell. 4, 1113–1120 (2022).
Islam, M. T. et al. Revealing hidden patterns in deep neural network feature space continuum via manifold learning. Nat. Commun. 14, 8506 (2023).
Vogelstein, J. T. et al. Supervised dimensionality reduction for big data. Nat. Commun. 12, 2872 (2021).
Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 25, 417–441 (1933).
Peng, D., Gui, Z., Gui, J., & Wu, H. A robust and efficient boundary point detection method by measuring local direction dispersion. IEEE Trans. Circuits Syst. Video Technol. https://doi.org/10.1109/TCSVT.2025.3546401 (2025).
Kruskal, J. B. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 29, 1–27 (1964).
Fisher, R. A. The use of multiple measurements in taxonomic problems. Ann. Eugenics 7, 179–188 (1936).
Yan, S. et al. Nonlinear discriminant analysis on embedded manifold. IEEE Trans. Circuits Syst. Video Technol. 17, 468–477 (2007).
Zhang, L., Zhou, W. & Chang, P.-C. Generalized nonlinear discriminant analysis and its small sample size problems. Neurocomputing 74, 568–574 (2011).
Tenenbaum, J. B., Silva, V. D. & Langford, J. C. A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000).
Roweis, S. T. & Saul, L. K. Nonlinear dimensionality reduction by locally linear embedding. Science 290, 2323–2326 (2000).
Cover, T. & Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 13, 21–27 (1967).
Belkin, M., & Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Proc. Advanced Neural Information Processing Systems (eds Dietterich, T. G. et al.) 585–591 (2001).
Donoho, D. L. & Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc. Natl Acad. Sci. USA 100, 5591–5596 (2003).
Coifman, R. R. et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc. Natl Acad. Sci. USA 102, 7426–7431 (2005).
van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).
McInnes, L., Healy, J., Saul, N. & Groçberger, L. UMAP: uniform manifold approximation and projection. J. Open Source Softw. 3, 861 (2018).
Becht, E. et al. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 37, 38–44 (2019).
Amid, E. & Warmuth, M. K. TriMap: large-scale dimensionality reduction using triplets. Preprint at https://arxiv.org/abs/1910.00204 (2022).
Fu, C., Zhang, Y., Cai, D. & Ren, X. AtSNE: efficient and robust visualization on GPU through hierarchical optimization. In Proc. 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD) 176–186 (Association for Computing Machinery, 2019).
Moon, K. R. et al. Visualizing structure and transitions in high-dimensional biological data. Nat. Biotechnol. 37, 1482–1492 (2019).
Kobak, D. & Berens, P. The art of using t-SNE for single-cell transcriptomics. Nat. Commun. 10, 5416 (2019).
Shen, C. & Wu, H.-T. Scalability and robustness of spectral embedding: landmark diffusion is all you need. Inf. Inference 11, 1527–1595 (2022).
Long, A. W. & Ferguson, A. L. Landmark diffusion maps (L-dMaps): accelerated manifold learning out-of-sample extension. Appl. Comput. Harmon. Anal. 47, 190–211 (2019).
Persad, S. et al. SEACells infers transcriptional and epigenomic cellular states from single-cell genomics data. Nat. Biotechnol. 41, 1746–1757 (2023).
Stanoi, I., Riedewald, M., Agrawal, D. & El Abbadi, A. Discovery of influence sets in frequently updated databases. In Proc. 27th International Conference on Very Large Databases (VLDB) (eds. Apers P. M. G. et al.) 99–108 (Morgan Kaufmann Publishers Inc., 2001).
Tao, Y., Papadias, D. & Lian, X. Reverse kNN search in arbitrary dimensionality. In Proc. 30th International Conference on Very Large Databases (VLDB) (eds Nascimento, M. A. et al.) 744–755 (Morgan Kaufmann Publishers Inc., 2004).
Radovanovic, M., Nanopoulos, A. & Ivanovic, M. Hubs in space: popular nearest neighbors in high-dimensional data. J. Mach. Learn. Res. 11, 2487–2531 (2010).
Loshchilov, I. & Hutter, F. SGDR: stochastic gradient descent with warm restarts. In Proc. 5th International Conference on Learning Representations (ICLR) 1769–1784 (Curran Associates, 2017).
Peng, D., Gui, Z. & Wu, H. MeanCut: a greedy-optimized graph clustering via path-based similarity and degree descent criterion. Preprint at https://arxiv.org/abs/2312.04067 (2023).
Karypis, G., Han, E.-H. & Kumar, V. Chameleon: hierarchical clustering using dynamic modeling. Computer 32, 68–75 (1999).
France, S. & Carroll, D. in Machine Learning and Data Mining in Pattern Recognition (ed. Perner, P.) vol. 4,571, 499–517 (2007).
Moor, M., Horn, M., Rieck, B. & Borgwardt, K. Topological autoencoders. In Proc. 37th International Conference on Machine Learning (ICML) (eds Daumé, H. & Singh, A.) 7045–7054 (PMLR, 2020).
Sainburg, T., McInnes, L. & Gentner, T. Q. Parametric UMAP embeddings for representation and semisupervised learning. Neural Comput. 33, 2881–2907 (2021).
Dua, D. & Graff, C. UCI machine learning repository. University of California Irvine https://archive.ics.uci.edu (2019).
Krizhevsky, A. & Hinton, G. Learning Multiple Layers of Features from Tiny Images Technical Report (Univ. Toronto, 2009).
Lecun, Y., Bottou, L., Bengio, Y. & Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998).
Xiao, H., Rasul, K. & Vollgraf, R. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. Preprint at https://arxiv.org/abs/1708.07747 (2017).
Corso, G. M. D., Gulli, A. & Romani, F. Ranking a stream of news. In Proc. 14th International World Wide Web Conference (WWW) 97–106 (Association for Computing Machinery, 2005).
Poličar, P. G., Stražar, M. & Zupan, B. openTSNE: a modular Python library for t-SNE dimensionality reduction and embedding. J. Stat. Softw. 109, 1–30 (2024).
Huang, H., Wang, Y., Rudin, C. & Browne, E. P. Towards a comprehensive evaluation of dimension reduction methods for transcriptomic data visualization. Commun. Biol. 5, 719 (2022).
Amir, E. A. et al. viSNE enables visualization of high dimensional single-cell data and reveals phenotypic heterogeneity of leukemia. Nat. Biotechnol. 31, 545–552 (2013).
Khan, S. A. et al. Reusability report: learning the transcriptional grammar in single-cell RNA-sequencing data using transformers. Nat. Mach. Intell. 5, 1437–1446 (2023).
Heng, J. S. et al. Hypoxia tolerance in the Norrin-deficient retina and the chronically hypoxic brain studied at single-cell resolution. Proc. Natl Acad. Sci. USA 116, 9103–9114 (2019).
Satija, R. et al. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 33, 495–502 (2015).
Kiselev, V. Y., Andrews, T. S. & Hemberg, M. Challenges in unsupervised clustering of single-cell RNA-seq data. Nat. Rev. Genet. 20, 273–282 (2019).
Peng, D. et al. Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity. Nat. Commun. 13, 5455 (2022).
Wang, S. K. et al. Single-cell multiome and enhancer connectome of human retinal pigment epithelium and choroid nominate pathogenic variants in age-related macular degeneration. Preprint at bioRxiv https://doi.org/10.1101/2025.03.21.644670 (2025).
Ziegler, C. G. et al. Impaired local intrinsic immunity to SARS-CoV-2 infection in severe COVID-19. Cell 184, 4713–4733 (2021).
Levine, J. H. et al. Data-driven phenotypic dissection of AML reveals progenitor-like cells that correlate with prognosis. Cell 162, 184–197 (2015).
Weber, L. M. & Robinson, M. D. Comparison of clustering methods for high-dimensional single-cell flow and mass cytometry data. Cytom. A 89, 1084–1096 (2016).
Ferrari, G., Thrasher, A. J. & Aiuti, A. Gene therapy using haematopoietic stem and progenitor cells. Nat. Rev. Genet. 22, 216–234 (2021).
Street, K. et al. Slingshot: cell lineage and pseudotime inference for single-cell transcriptomics. BMC Genomics 19, 477 (2018).
Trapnell, C. et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 32, 381–386 (2014).
Young, W. J. et al. Genetic analyses of the electrocardiographic QT interval and its components identify additional loci and pathways. Nat. Commun. 13, 5144 (2022).
Niroshana, S. M. I., Kuroda, S., Tanaka, K. & Chen, W. Beat-wise segmentation of electrocardiogram using adaptive windowing and deep neural network. Sci. Rep. 13, 11039 (2023).
Huo, R. et al. ECG segmentation algorithm based on bidirectional hidden semi-Markov model. Comput. Biol. Med. 150, 106081 (2022).
Oberlin, T., Meignen, S. & Perrier, V. The Fourier-based synchrosqueezing transform. In Proc. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 315–319 (IEEE, 2014).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Laguna, P., Mark, R. G., Goldberg, A. & Moody, G. B. A database for evaluation of algorithms for measurement of QT and other waveform intervals in the ECG. Comput. Cardiol. 24, 673–676 (1997).
Goldberger, A. L. et al. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation 101, e215–e220 (2000).
Bengio, Y., Courville, A. & Vincent, P. Representation learning: a review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828 (2013).
Peng, D., Gui, Z. & Wu, H. Interpreting the curse of dimensionality from distance concentration and manifold effect. Preprint at https://arxiv.org/abs/2401.00422 (2023).
Healy, J. & McInnes, L. Uniform manifold approximation and projection. Nat. Rev. Methods Primers 4, 82 (2024).
Malkov, Y. A. & Yashunin, D. A. Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs. IEEE Trans. Pattern Anal. Mach. Intell. 42, 824–836 (2018).
Dong, W., Moses, C. & Li, K. Efficient k-nearest neighbor graph construction for generic similarity measures. In Proc. 20th International Conference on World Wide Web (WWW) 577–586 (Association for Computing Machinery, 2011).
Saul, L. K. & Roweis, S. T. Think globally, fit locally: unsupervised learning of low dimensional manifolds. J. Mach. Learn. Res. 4, 119–155 (2003).
Wang, J. Real local-linearity preserving embedding. Neurocomputing 136, 7–13 (2014).
Wang, Z. et al. Clustering by local gravitation. IEEE Trans. Cybern. 48, 1383–1396 (2018).
von Luxburg, U. A tutorial on spectral clustering. Stat. Comp. 17, 395–416 (2007).
Ding, J., Shah, S. & Condon, A. densityCut: an efficient and versatile topological approach for automatic clustering of biological data. Bioinformatics 32, 2567–2576 (2016).
Kuhn, H. W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 2, 83–97 (1955).
Peng, D. Source code of SUDE. Zenodo https://doi.org/10.5281/zenodo.16792257 (2025).
Peng, D. Open code for in-review “Sampling-enabled scalable manifold learning unveils discriminative cluster structure of high-dimensional data”. Code Ocean https://doi.org/10.24433/CO.9866909.v3 (2025).
AI Research
NFL player props, odds, lines: Week 2, 2025 NFL picks, SportsLine Machine Learning Model AI predictions, SGP

The Under went 12-4 in Week 1, indicating that not only were there fewer points scored than expected, but there were also fewer yards gained. Backing the Under with NFL prop bets was likely profitable for the opening slate of games, but will that maintain with Week 2 NFL props? Interestingly though, four of the five highest-scoring games last week were the primetime games, so if that holds, then the Overs for this week’s night games could be attractive with Week 2 NFL player props.
There’s a Monday Night Football doubleheader featuring star quarterbacks like Baker Mayfield, C.J. Stroud and Justin Herbert. The games also feature promising rookies such as Ashton Jeanty, Omarion Hampton and Emeka Egbuka. Prop lines are usually all over the place early in the season as sportsbooks attempt to establish a player’s potential, and you could take advantage of this with the right NFL picks. If you are looking for NFL prop bets or NFL parlays for Week 2, SportsLine has you covered with the top Week 2 player props from its Machine Learning Model AI.
Built using cutting-edge artificial intelligence and machine learning techniques by SportsLine’s Data Science team, AI Predictions and AI Ratings are generated for each player prop.
Now, with the Week 2 NFL schedule quickly approaching, SportsLine’s Machine Learning Model AI has identified the top NFL props from the biggest Week 2 games.
Week 2 NFL props for Sunday’s main slate
After analyzing the NFL props from Sunday’s main slate and examining the dozens of NFL player prop markets, the SportsLine’s Machine Learning Model AI says Lions receiver Amon-Ra St. Brown goes Over 63.5 receiving yards (-114) versus the Bears at 1 p.m. ET. Detroit will host this contest, which is notable as St. Brown has averaged 114 receiving yards over his last six home games. He had at least 70 receiving yards in both matchups versus the Bears a year ago.
Chicago allowed 12 receivers to go Over 63.5 receiving yards last season as the Bears’ pass defense is adept at keeping opponents out of the endzone but not as good at preventing yardage. Chicago allowed the highest yards per attempt and second-highest yards per completion in 2024. While St. Brown had just 45 yards in the opener, the last time he was held under 50 receiving yards, he then had 193 yards the following week. The SportsLine Machine Learning Model projects 82.5 yards for St. Brown in a 4.5-star pick. See more Week 2 NFL props here.
Week 2 NFL props for Vikings vs. Falcons on Sunday Night Football
After analyzing Falcons vs. Vikings props and examining the dozens of NFL player prop markets, the SportsLine’s Machine Learning Model AI says Falcons running back Bijan Robinson goes Over 65.5 rushing yards (-114). Robinson ran for 92 yards and a touchdown in Week 14 of last season versus Minnesota, despite the Vikings having the league’s No. 2 run defense a year ago. The SportsLine Machine Learning Model projects Robinson to have 81.8 yards on average in a 4.5-star prop pick. See more NFL props for Vikings vs. Falcons here.
You can make NFL prop bets on Robinson, Justin Jefferson and others with the Underdog Fantasy promo code CBSSPORTS2. Pick at Underdog Fantasy and get $50 in bonus funds after making a $5 wager:
Week 2 NFL props for Buccaneers vs. Texans on Monday Night Football
After analyzing Texans vs. Buccaneers props and examining the dozens of NFL player prop markets, the SportsLine’s Machine Learning Model AI says Bucs quarterback Baker Mayfield goes Under 235.5 passing yards (-114). While Houston has questions regarding its offense, there’s little worry about the team’s pass defense. In 2024, Houston had the second-most interceptions, the fourth-most sacks and allowed the fourth-worst passer rating. Since the start of last year, and including the playoffs, the Texans have held opposing QBs under 235.5 yards in 13 of 20 games. The SportsLine Machine Learning Model forecasts Mayfield to finish with just 200.1 passing yards, making the Under a 4-star NFL prop. See more NFL props for Buccaneers vs. Texans here.
You can also use the latest FanDuel promo code to get $300 in bonus bets instantly:
Week 2 NFL props for Chargers vs. Raiders on Monday Night Football
After analyzing Raiders vs. Chargers props and examining the dozens of NFL player prop markets, the SportsLine’s Machine Learning Model AI says Chargers quarterback Justin Herbert goes Under 254.5 passing yards (-114). The Raiders’ defense was underrated in preventing big passing plays a year ago as it ranked third in the NFL in average depth of target allowed. It forced QBs to dink and dunk their way down the field, which doesn’t lead to big passing yardages, and L.A. generally prefers to not throw the ball anyway. Just four teams attempted fewer passes last season than the Chargers, and with L.A. running for 156.5 yards versus Vegas last season, Herbert shouldn’t be overly active on Monday night. He’s forecasted to have 221.1 passing yards in a 4.5-star NFL prop bet. See more NFL props for Chargers vs. Raiders here.
How to make Week 2 NFL prop picks
SportsLine’s Machine Learning Model has identified another star who sails past his total and has dozens of NFL props rated 4 stars or better. You need to see the Machine Learning Model analysis before making any Week 2 NFL prop bets.
Which NFL prop picks should you target for Week 2, and which quarterback has multiple 5-star rated picks? Visit SportsLine to see the latest NFL player props from SportsLine’s Machine Learning Model that uses cutting-edge artificial intelligence to make its projections.
AI Research
What Is One of the Best Artificial Intelligence (AI) Stocks to Buy Now? – The Motley Fool
AI Research
Artificial Intelligence in Trauma and Orthopaedic Surgery: A Comprehensive Review From Diagnosis to Rehabilitation
-

 Business2 weeks ago
Business2 weeks agoThe Guardian view on Trump and the Fed: independence is no substitute for accountability | Editorial
-
Tools & Platforms1 month ago
Building Trust in Military AI Starts with Opening the Black Box – War on the Rocks
-

 Ethics & Policy2 months ago
Ethics & Policy2 months agoSDAIA Supports Saudi Arabia’s Leadership in Shaping Global AI Ethics, Policy, and Research – وكالة الأنباء السعودية
-

 Events & Conferences4 months ago
Events & Conferences4 months agoJourney to 1000 models: Scaling Instagram’s recommendation system
-

 Jobs & Careers3 months ago
Jobs & Careers3 months agoMumbai-based Perplexity Alternative Has 60k+ Users Without Funding
-

 Podcasts & Talks2 months ago
Podcasts & Talks2 months agoHappy 4th of July! 🎆 Made with Veo 3 in Gemini
-

 Education2 months ago
Education2 months agoVEX Robotics launches AI-powered classroom robotics system
-

 Education2 months ago
Education2 months agoMacron says UK and France have duty to tackle illegal migration ‘with humanity, solidarity and firmness’ – UK politics live | Politics
-

 Podcasts & Talks2 months ago
Podcasts & Talks2 months agoOpenAI 🤝 @teamganassi
-

 Funding & Business3 months ago
Funding & Business3 months agoKayak and Expedia race to build AI travel agents that turn social posts into itineraries